 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Preface: The shootdown of MH17 has been bothering me a great deal.
Within a minute of learning of it last Thursday at lunchtime, I knew pretty much what happened and why.
One way I cope with such situations is to make them into a teaching moment, using simple math and physics, relating to ordinary things in people’s lives.
I did a lot of that after 9/11, and again after Columbia.
Update: On 13 October 2015, the Dutch Safety Board released its final report definitely identifying the SA-11 as the weapon which brought down the plane.
Enquiring minds have been asking on the [FPSpace] forum whether the SA-11 missile that killed MH17 could have been seen by US space-based assets. Russian officials have expressed skepticism (disingenuously, in my opinion) that such a detection would not be possible. (If you're not patient enough to read thru to the end, the short answer is, of course it was seen.)
In the interest of shedding light, not heat, I did a BOTE
(back o’ the envelope, along the lines of “consider a spherical cow”) estimate
of the visibility from space of the thermal emission of an SA-11 launch. Based
on first principles, and not too many SWAGs, the
answer is “yes”.
I consulted my ancient desktop manual “Illustrated Dictionary of Modern Soviet
Weapons” (Prentice Hall Press, 1986), and compared it to the table
of specs in the wiki to be sure we’re talking about
the same thing. Yes, what the Russkiis call the “9M38” under their GRAU system of military nomenclature aka “Buk” which means “Beech”[tree] is what the US DoD/NATO calls the GADFLY/SA-11. A more advanced version of the Buk air defense system
is called GRIZZLY or SA-17 by NATO. For the purpose of this analysis, the SA-11 and SA-17 are very similar in mass and length.
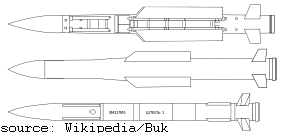
|
9М38 |
|
|
Comparison
of 9M38M1, 9M317 and 9M317ME surface-to-air missiles of the Buk missile system |
|
|
Type |
|
|
Place of origin |
Soviet Union |
|
Production
history |
|
|
Variants |
9М38, 9М38M1, 9M317 |
|
Specifications
(9М38, 9M317) |
|
|
Weight |
690 kg, (1521 Lbs) 715 kg,(1576
Lbs) |
|
Length |
5.55 m (18'-3") |
|
Diameter |
0.4 m (15 3/4") (wingspan 0.86 m)(2'-10") |
|
Warhead |
Frag-HE |
|
Warhead weight |
70 kg,(154.3 Lbs) |
|
Detonation |
|
|
|
|
|
Propellant |
|
|
Operational |
30 kilometres (19 mi) |
|
Flight altitude |
14,000 metres
(46,000 ft) |
|
Speed |
Mach 3 |
|
Guidance |
|
|
Launch |
See structure |
So GLOW is 700 kg, with a 70 kg warhead (red-colored part in the figure below). Figure 500 kg of propellant (orange-colored part in the figure below), all solid, burning in 15 secs. Allocate 130 kg for everything else, airframe, fins, avionics/fuze/guidance, etc. (Gray-colored parts in the figure below.) No air breathing in this case (although a few Soviet-era SAMs did do that); all of Buk’s propellant (fuel blended with oxidizer) is onboard.
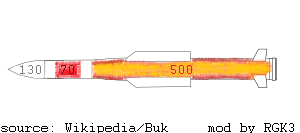
500 kg in 15 sec is an average burn rate of 33
kg/sec. But the wiki says:
The 9M38
surface-to-air missile utilizes a two-mode solid fuel rocket engine with total burn time of about 15
seconds; the combustion
chamber is reinforced by metal.
I’m guessing the two modes are
“boost” to rapidly accelerate to Mach 3, then “sustain” at a much lower burn
rate just enough to maintain velocity, overcome drag, gain altitude, and make
rapid course changes but not accelerate the missile any more.
The maximum engagable
target speed was 1200 m/s and it [the 9M317 version] can tolerate an
acceleration overload of 24G.
We’ll partition the burn into 5
seconds of boost @ 20 gravities (a very hard ride, practically a controlled explosion), which gets the missile to 1000 m/s i.e., Mach 3.
This is followed by 10 seconds of sustaining burn @ 0 gee net after MECO. I note the older
SA-2 system also had a boost phase of about 5 seconds plus a dozen-and-a-half
seconds of sustainment, so that’s a reasonable time partition. To keep the math simple, we'll assume a launch straight up.
What kind of energy are we talking about in the launch
plume, and what’s its energy partition?
Let’s assume a really
high-performance solid rocket propellant has an energy density similar to TNT,
i.e. 1 kcal per gram. Unlike food or gasoline, but like explosives, rocket
propellant must contain its own oxidizer. (Side note: Butter for example has way more energy than TNT, nine kcal per gram, not just one, because the air to oxidize it
isn’t in the stick. Moreover the energy released by
oxidizing the stick in your stomach is roughly equal to lifting that butter
into low Earth orbit.) Rocket designers have an interest in clean stoichiometry so we can assume the fuel is
fully burned for max heat release. OK, Wiki confirms the number
for TNT in SI units:
The explosive energy [for TNT] utilized by NIST is 4184 J/g (4.184 MJ/kg).[16]
So, excluding the warhead, the
initial energy contained in the propellant is 500 [kg] x 1000 [g/kg] x 4184
joules [J/g], or 2 billion joules (2 gigajoules). Figure the burn rate during boost is an order of magnitude
greater than the sustaining rate. So we’ll divvy it up
thus: 80 kg/sec x 5 seconds of boost plus 10 kg/sec x 10 seconds of sustain,
then the propellant’s gone. Based on SA-2 experience, that’s
a reasonable assumption.
Assuming the missile is launched straight up, then at MECO (main engine cut off)*
when 80% of the propellant is burned (1.6 out of the 2 gigajoules is used up),
the missile’s parameters are: mass* = 300 kg*, speed = 1000 m/sec, altitude =
2500 m*.
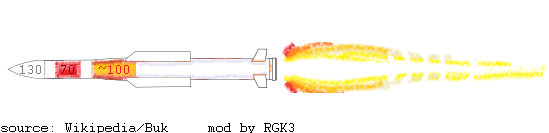
Energy of position at MECO is m * g * h = 300 x 10 x 2500 =
7.5 megajoules. Energy of motion at MECO is 1/2 * m * v2 = 1/2 * 300 x 10002 =
150 megajoules. (Without atmospheric drag, the
missile could coast straight upward without further boost for another 50 km before
coming to a stop.) Energy lost to drag: it is difficult to estimate this term
on the back of an envelope for an intelligent layman,
but comparing the power during the boost burn rate versus the power during the
sustaining burn rate suggests that drag loss is roughly a tenth of the total
energy budget until now. So, 160 megajoules.
That’s a SWAG. Adding these up gives you about 320 megajoules,
which is only 20% of the 1.6 gigajoules of energy in the propellant burned so
far. And only half of that, 10%, is in the form of
actually useful speed and height. Mostly speed. Rockets are not very efficient**! See the Sankey*** diagram below.
(*Once the sustainment propellant is gone, mass at burnout would be 200 kg. We know the “service
ceiling” (some service!) of the SA-11 is better than 20 klicks,
and I already showed that the missile could get very high just by
coasting. But I haven’t bothered to estimate
burnout velocity or height. At Mach 3 or 1 km/sec, it can get everywhere it’s aimed within 20 or 30 seconds, but it’s also clear that
all the action with respect to infrared detection by satellite is during the
boost phase.)
(***Sankey diagrams, which depict flow rates proportional to the width of the arrow,
were invented by the great Irish engineer Matthew Henry Phineas Riall Sankey at the turn of the last century.
One Sankey diagram is worth a thousand pie charts.)
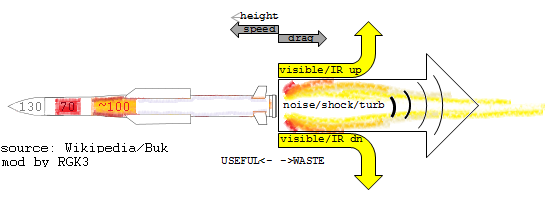
So, 10% useful work and the same
lost to drag leaves 80% x 1.6 gigajoules = ~1.3 GJ being dissipated to the
environment. We know that this energy is being wasted,
but how?
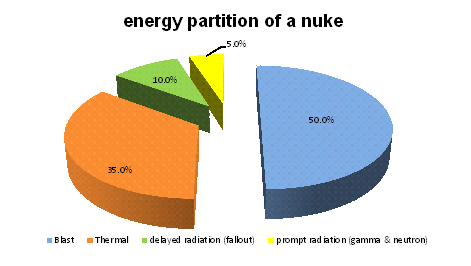
Recall the rule of thumb that the energy partition of a
nuclear explosion is typically about one-half mechanical blast, one-third thermal
radiation, and one-sixth nuclear radiation (prompt gamma rays and neutrons, plus
delayed radiation, i.e., fallout). The ratio between blast and thermal in a nuke is 1.5-to-1.
That partition is driven by the extreme temperature of the
initial fireball, millions then thousands of degrees. By contrast, the incandescent
rocket exhaust from a chemical reaction might be 5000 kelvins, max. So I think it’s safe to estimate that the partition of
wasted energy in a rocket’s exhaust plume is at least 2:1 mechanical effects
(shock/noise/turbulence) relative to thermal effects (mostly radiation). The
time scale is so short that I don’t think conduction
to the surrounding air is a significant heat loss mechanism, and convection
(heat loss by swirling fluid) sort of bridges the gap between mechanical and
thermal. So let’s just say 2:1. See the Sankey diagram above.
2:1 means two-thirds (800+ megajoules)
become noise, etc, and one-third of the waste (400+ megajoules)
becomes light then heat. Let’s assume a steady-state
burn over those 5 seconds of rapid boost. Dividing 400 MJ by 5 seconds means
the average radiated optical power is ~80 megawatts. The acoustic/mechanical
power is double that.
[Interesting interim fallout: 80 kg/sec combustion yields 80
MW radiant power, i.e. 1 kg/sec --> 1
MW optical power. That’s a useful, easy-to-remember
metric. All you have to know is a rocket’s fuel mass and burn time, and you can figure out its effective power in your
head.]
All this power is being dumped into a teardrop-shaped volume
perhaps a meter or three at its widest by 10 meters or so long. Say 15 square meters
projected area from almost any angle. Another SWAG.
The visible incandescent part at 5000 kelvins is a lot smaller than the smoky
part. The visible part cools off not just by expansion but
extremely fast by radiation (proportional to T4). But
even the smoky part will radiate in the infrared for a few seconds more. How
much longer requires an extremely technical analysis and a
lot of assumptions we won’t bother with. We could back into an estimate
of the color temperature with the given energy, mass flow, and a blackbody
curve, but it’s not worth the trouble. We have enough to proceed to an answer.
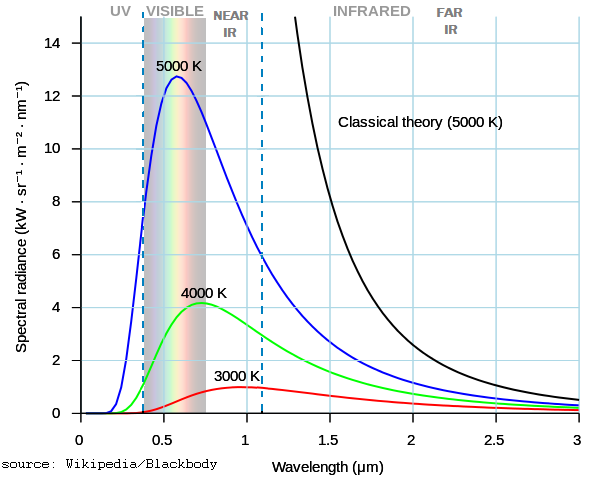
As you can see from this blue curve on this graph, a
blackbody radiating at 5000K puts well over half its total emissive power (63%
≈ 1-1/e) counting the area under the curve and within the interval between the
two vertical dashed blue lines, 400-nm violet light on the left and 1100-nm
near IR on the right. Even a cool 3000K flame (red curve) puts about half its
power in the wavelengths that military satellites can see.
Shape and aspect ratio are important when trying to see something,
but only at short range. A unobstructed rear view
would be better than a front view, since the body of the missile will occult
some of its own plume, while a side-on view of the long hot plume would be best
of all. But I’m guessing that aspect ratio would make
at most a factor of 2 or 3 difference at modest range, not more. From a long
distance away, the exhaust plume is pretty much a point source, so we can
assume half the thermal radiation (~40+ MW) goes into a hemisphere aimed down,
and the other half (~40+ MW) goes up into space. Long-wave IR from warm
surfaces gets trapped pretty effectively by our
atmosphere, but pretty hot short-wave near-IR stuff does not (which is why the
greenhouse effect works and keeps us alive). If it’s
hot enough, heat goes out as easily as it came in. Before our “eye in the sky”
sees it, at least one-sixth or so of the visible/near-IR radiation gets filtered or absorbed by the air above it, even on a
clear day. On a cloudy day, no IR might make it out, so cloud cover is an
important factor for detecting light and heat, but not radio. Accounting for
this further loss still leaves optical power in the mid-30s of megawatts, of
which about 2/3 is stuffed into wavelengths that military birds in space can
see. So let’s say ~20+ MW of thermal power spreads isotropically out into space from the moving point source
under decent viewing conditions. Since the sky was clear enough for the killers
to see up to their target, it was clear enough to see down, too. Cuts both ways.
So the task becomes to see a 15-square-meter object
radiating like a 5000K blackbody at ~20+ MW in the visible and the near-IR for
5 seconds. Say a surface emission intensity of >1
MW per square meter, possibly as much as 2 MW/m2. Well, compare this to the typical
surface intensity from our warm Earth radiating at 300K: 250-350 W/m2, summed over all waves, depending when and where you
measure from. So from low orbit the SA-11’s hot
exhaust plume is optically 3,000-8,000 times brighter than Earth’s warm background
disk, i.e. a signal-to-noise ratio of 35-39 decibels.
Is a thermal signal with this much contrast visible from
deeper in space, say from the old Defense Support Program (DSP) satellites in
GEO, which were designed 40+ years ago to detect strategic missile launches
during the Cold War?
Remember that an optical system like a telescope is a light
bucket. That is, it collects,
it integrates. This is why stars are
visible to our human eyeballs as point sources, even though their actual disks
are way too small to make out with such tiny pupils.
So a hot spot buried inside a pixel (not to be confused with a “hot pixel”
which is a technical malfunction astrophotographers grapple with) can bleed over and bump up the brightness
value of the whole pixel across the detectable threshold even if the hot spot
is way smaller than the ostensible resolution of the imaging system. The amount
of the bump is straight arithmetic averaging over the area. From close up, what
looks like one hot spot emitting X, next to a cold one emitting nothing, will
from far off look like a spot twice the area emitting the average of the two,
i.e., X/2.
Operators of commercial remote sensing satellites (in 800-km
LEO) have recently announced the availability of resolution at 30 cm. (It is an open secret that US reconnaissance satellites at one time
could achieve about half this figure; perhaps they still can.)
Commercial systems have optical elements in the range of 1 meter across; civil
scientific birds like Hubble can go more than twice that. Since resolution
scales linearly with distance, that means the same imaging bird with the same
size optics directly overhead in GEO, 45X further away, should be able to make
out a pixel roughly 15 m across (and maybe half that) in visible light.
Unfavorable geometry (viewing from off-axis) makes less difference in GEO than
it would in LEO, because from a spot in GEO everything is more-or-less the same
distance away (within +/- 10%). Now, resolution also
scales directly with wavelength, so a 15-m pixel from GEO at 550 nanometers
(yellow-green light) becomes a 30-m pixel at 1100 nanometers (near-infrared light). Since the old Cold War systems were
looking in the IR, we’ll use the tougher parameter and
also assume no-better-than-known-modern civilian technology.
The area of a 30-meter-wide pixel is a bit over 700 square
meters. Arithmetically blending a 20-MW / 15-sq.meter hot source into that 700 sq.meter area “cools down” the
brightness ratio by a factor of 45 or so. Thus, from GEO, a pixel with an
SA-11’s hot launch plume blended into it should still be about 60-170X as
bright as any neighboring pixel of the warm Earth, i.e. a SNR of 18-22
decibels. Say, 20 dB.
20 dB is a good solid signal. Even
40-year-old Cold War technology would have bagged that shot.
If SBIRS (a newer much more capable system with some portions in
Molniya orbits that swoop much closer to the ground) happened to be in the
right place, then it assuredly saw the missile launch and the destruction of
MH17, too.
QED.
No taking things on faith, absurd press releases or ignorant
lame-*ss blogs required; the application of simple
logic, math and physics by our own minds tells us what us need to know.
Robert Kennedy is president of the Ultimax Group Inc., a corporation distributed across 11 time zones from Moscow to L.A. He speaks enough languages to start bar fights in all of them. Robotics engineer, amateur historian, and jack of all trades, he spent 1994 working for the House Science Committee's Subcommittee on Space as ASME's Congressional Fellow. Robert lives in Oak Ridge, Tennessee, where he resides with his wife, numerous cats, and a whole lot of Detroit iron.
[var86]. various, Illustrated Dictionary of Modern Soviet Weapons, (Prentice Hall Press 1986)
More recent “Buk” information from en.wikipedia.org/wiki/Buk_missile_system
17-24Jul2014: original private analysis offline
24Jul2014: upload HTML version to Web.
27Jul2014: modify and adapt images, Sankey diagram, and upload.
13Oct2015: Dutch Safety Board releases final report identifying the SA-11 at the weapon which brought down the aircraft.
21Oct2015: corrected location of warhead at top of body, not cone.
Back to Directory of White Papers
For product or dealer inquiries within the USA & Canada, call:
West Coast: (888) ULTIMAX..................................................................East Coast: (800) ULTIMAX
Outside USA: +1 (865) 405-5806
or write to us:
The Ultimax Group, Inc.
112 Mason Lane
Oak Ridge, Tennessee, USA 37830-8631
or send email to robot at ultimax dot com
The entire content (text and images except those sourced as noted) of these pages is copyrighted and may not be distributed, downloaded, modified, reused, re-posted or otherwise used without the express written permission of the authors.
Privacy Policy: The Ultimax Group Inc., will never sell our customer list or distribute our customer's personal data to others without permission.
These pages last updated October 21, 2015